
SrTiO3 (001) etching

SrTiO3 (001) etching
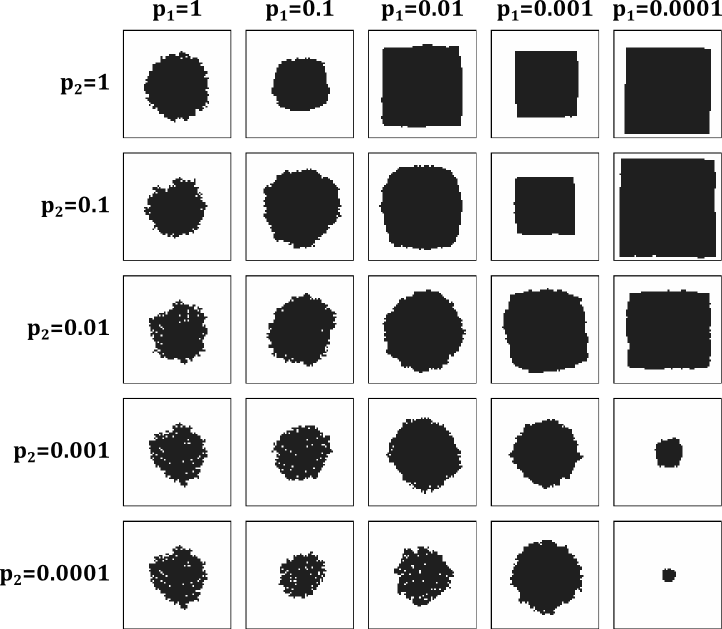
Fig. 1: Simulated etch pit shapes for various etching parameters

Fig. 2: starting image for pit shape simulations
The starting image (Fig. 2) for the etch pit shape simulations just contained a small 5 x 5 unit cell pit in the middle of the 256 x 256 unit cell etch area. Note that etching times (number of Monte Carlo steps) varied for different simulations.
The etching probabilities of isolated unit cells were assumed to be high, i.e., p3=1 and p4=1. Etching probabilities were varied only for the edge and corner sites.
As the simulated pi shapes show, realistic etching results are obtained when the corner or kink sites have at least 10 times higher probability of being etched that straight edge sites. Nearly straight pit edges are obtained, for example, if p(1)=0.1 and p(2)=1. This means that a single unit cell is removed from an otherwise straight step edge and etching then proceeds very quickly along the edge until a corner is reached. This way the etch pit grows while maintaining a square shape.
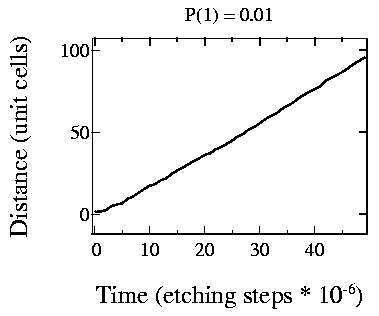
Fig. 3: Step edge movement speed
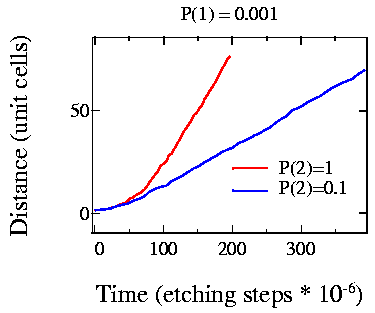
Fig. 4: Comparing the effect of kink site etching rate change
If etching probabilities for straight edge sites (one free edge) and kink sites (two free edges) become comparable, the pit becomes round. If kink site etching probability is lower than the straight edge site etching probability, the etch pit shape will become irregular.
It is also interesting to plot etching speeds for relevant parameter combinations. Looking at Fig. 3, where p1=0.01 and p2=1, i.e., it is 100 times more probable that a kink site is etched than a straight site. The growth of the etch pit is nearly linear, except at the very beginning.
The effect of kink site stability on the shape of small etch pits is more clearly visible in Fig. 4. The etching probabilities are shown in the figure and it is clear that the quadratic growth region is more pronounced for higher kink site etching rates (large p2). Small pits, with a size of up to about 15 unit cells grow quadratically. After that, the pit growth is linear in time.
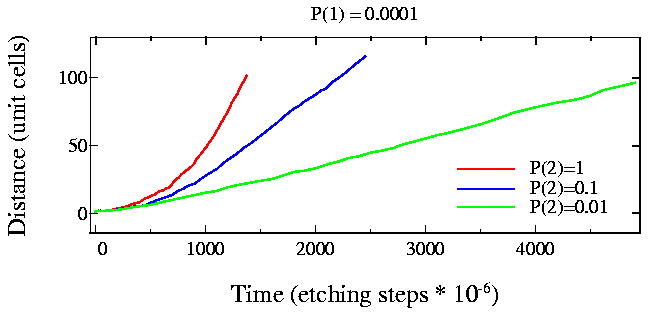
Fig. 5: Step edge motion for very fast kink-site etching rates
The quadratic growth region is clearly visible in the last simulation (Fig. 5), particularly for the case where p1=0.0001 and p2=1, i.e., the etching probability ratio for the stratight and kink sites is 10000.
The presence of two growth types, quadratic and linear, can be explained by considering the effect of the size of the etch pit on etching speed. If the etch pit is small and it is much easier to remove a unit cell from a kink site than from a straight site, etching occurs as shown in the following animation:

Fig. 6: Step-flow etching of a small pit
Etching starts by removing a unit cell from a straight site. This forms two kink sites on either side of the removed unit cell. The probability of these kink sites to be etched is very high, so etching quickly proceeds until the edges of the pit are reached. Because the probability of removing a unit cell from a straight site is very low, a full row of unit cells is always removed before another straight site is etched. Etching speed is in this case proportional to the total length of the etch pit edge and grows quadratically in time.
As the size of the etch pit grows, it also takes more time to clear away one row of unit cells from the pit edge. At some stage it becomes probable that two (or more) unit cells are removed from straight sites on the same edge before kink site etching ends at the pit edges. In this case the etching speed no longer depends on the pit size. Etching speed is now determined only by the straight site etching probability and etch speed is linear in time. Etching occurs as shown below:

Fig. 7: Step-flow advance of a long edge
If the probability of removing a unit cell from a straight site per unit time is p1, the time between two straight edge removals is, on average, t1=1/(n p1), where n is the number of unit cells on an edge (the width of an etch pit). Obviously, this time gets smaller as the etch pit edge length increases.
The amount of time, on average, required to remove a kink site is t2=1/p2, where p2 is the etching probability of a kink site. The time required to remove all kink sites along the edge after a straight site has been etched is te=(n-1)/p2. This time grows as the etch pit edge becomes longer.
At some critical value of nc the times t1 and te become equal, nc2=p2/p1. If this transition from quadratic growth to linear growth can be observed by AFM, it should be possible to determine the ratio of the straight site and kink site etching probabilities. Etching speed in the linear regime would give the absolute scaling for the straight site etching probability p1. In reality, the straight site and kink site etching probabilities are rather close, so the quadratic growth region may not be detectable at all in practice.